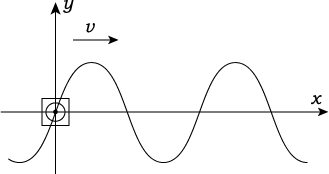
偙偙偱偼偄傢備傞乽惓尫攇乿偲屇偽傟傞攇偺幃偵偮偄偰傗偭偰偄偒傑偡丅
崅峑惗偺斖埻側偺偱偡偑丄偡偭偛偔曄側僇儕僉儏儔儉偵側偭偰偄偰丄
攇偺幃偺婎杮偲側傞乽扨怳摦乿偺曽偑偁偲偵棃傞偲偄偆僇僞僠傪偲偭偰偄傑偡丅
偪側傒偵嫵壢彂偱偼價儈儑乣偵棳偟偰偄傑偡丅乮偍偦傜偔僙儞僞乕帋尡斖埻偵偟偨偐偭偨偩偗偱偟傚偆乯
庢傝姼偊偢丄乽扨怳摦乿傪傗偭偰偄傞偲偄偆慜採偱傗偭偰偄偒傑偡丅
惓尫攇偲偄偆偺偼丄奺攠幙偺扨怳摦偵傛傞埵憡偺僘儗偵傛偭偰婲偒傞傕偺偱偁傞丅
攇偺幃傪峫偊偰偄偔栿偩偑丄攇偵偼擇偮偺僌儔僼偑偁傞丅丂偦傟偼丄
攇宍偺僌儔僼偲扨怳摦偺僌儔僼偱偁傞丅
偁傞X偱偺攠幙偺扨怳摦偺僌儔僼丅偁傞俿偱偺攇宍偺僌儔僼丅
偮傑傝丂攇偺幃偼擇曄悢娭悢偲側傞丅
傑偨丂尨揰偱偺扨怳摦偼偡傋偰偺揰偺扨怳摦偲摨堦偱偁傞丅
壓偺條側僌儔僼傪峫偊傞丅

偙傟偼t=t1偵偍偗傞攇宍偺僌儔僼偱偁傞丅攇偺懍搙傪v偲偟丄栴報偺曽岦偵恑傫偱偄傞偲偡傞丅
師偵埥傞帪娫偨偭偨僌儔僼傪峫偊傞丅
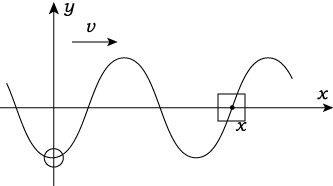
t=t1偺偲偒尨揰偵偁偭偨仩偼埥傞帪崗宱偭偨僌儔僼偱偼x偺埵抲偵棃偰偄傞丅
攇偼v偱恑傫偱偄傞偙偲傪峫偊傞偲丄埥傞帪崗偲偼丂t=t1+x/v偱偁傞帠偑暘偐傞丅
偙偙偱尨揰偺扨怳摦偲丄X偵偍偗傞扨怳摦偵拝栚偡傞丅
t=t1偺偲偒尨揰偵偁偭偨仩偼t=t1+x/v偺偲偒丄X偵偁傞丅
偲偄偆偙偲偼丄尨揰偱t=t1偐傜尒偨扨怳摦偲丄
丂丂丂丂丂丂丂丂X偱t=t1+x/v偐傜尒偨扨怳摦偼
丂丂丂丂丂丂丂丂摨堦偺塣摦傪偟偰偄傞丅
偮傑傝丄X偵偍偗傞扨怳摦偼尨揰偱偺儮t=x/v慜偺扨怳摦偲摨偠偱偁傞丅
尨揰偱偺扨怳摦偺幃傪
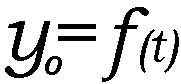
偲偡傞偲丄X偱偺扨怳摦偺幃偼丄尨揰偱偺儮t=x/v慜偺扨怳摦偺幃偲摨偠偱偁傞偐傜丄
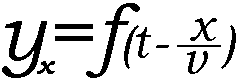 丒丒丒嘆
丒丒丒嘆
偲側傞丅尨揰偱偺扨怳摦偺幃傪
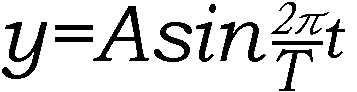
偲偟丄廃婜傪T丄攇挿傪兩偲偡傞偲丄嘆幃偼師偺傛偆偵弌棃傞丅
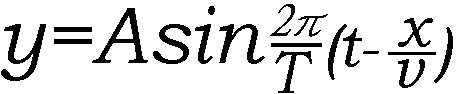
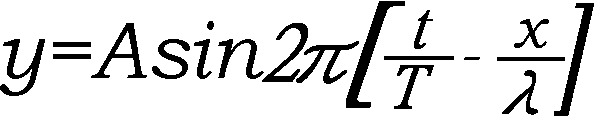
偲側傝丄椺偺幃偑弌偰偔傞丅
仈偪側傒偵丂t偺崁偲x偺崁傪媡偝傑偵偟偪傖偆恖懡偄偐傜丄妎偊曽偹丅
僩僫僇僀乮T乯偼儔僋僟乮兩乯傛傝憗偄乮敋乯
偄偠傚両